In unserer Modellwelt gibt es die Erde und einen Ball. Die Erde beschleunigt den Ball durch die Gewichtskraft nach unten. Sonst gibt es in unserer Modellwelt keine Kräfte. Unser Modell-Ball hat keine Ausdehnung, sodass er sich nicht drehen kann und selbst dann nicht gebremst würde, wenn es in unserem Modell Luft gäbe. Unser Modell-Ball ist also eigentlich gar kein richtiger Ball, sondern ein Punkt in einer 2D-Welt.
Uns ist also bewusst: unser ausgedachtes Modell ist deutlich simpler als die reale Welt. Es ist fast schon erstaunlich, wie gut dieses einfache Modell reale Flugkurven trotzdem beschreibt. Jenachdem, welche Wurfbewegung ihr gewählt und beobachtet habt, seht ihr aber auch deutliche Unterschiede zwischen der von euch simulierten Flugkurve und der tatsächlich beobachteten. Wir können uns also fragen: wie können wir weitere Gegebenheiten der realen Welt in unserem Modell berücksichtigen, sodass die Prognosen aus dem Modell noch besser mit unseren tatsächlichen Beobachtungen übereinstimmen?
Auf dieser Seite findet ihr hierzu verschiedene Infos.
Anfangs- und Randwerte
Wenn ihr feststellt, dass die nach eurem Modell simulierten Werte für die Flugkurve nicht mit der beobachteten Flugkurve übereinstimmen, könnt ihr zunächst prüfen, ob es vielleicht an den Anfangs- und Randwerten liegt – hierzu müsst ihr das Modell gar nicht ändern. Die in der Simulation geschätzten Anfangswerte für eure Wurfbewegung sind ja eben nur geschätzt.
Könnt ihr die Anfangswerte (Ort und Geschwindigkeit in x- und y-Richtung) so ändern, dass eure simulierte Bahnkurve besser zu der beobachteten passt?
Tipp: bei jeder neuen Simulation mit anderen Anfangswerten erhöht die Variable „Nr“ in eurer Simulation. Dann überschreibt ihr eure alten Ergebnisse nicht, sondern könnt diese später vergleichen.
Luftreibung
In der realen Welt hat der Ball eine Ausdehnung und bewegt sich durch Luft. Um dies mit unserem Modell zu simulieren, können wir auch in unserem Modell Luftreibung ergänzen. Wir beschreiben Luftreibung als Kraft, die auf den Ball entgegen seiner Bewegungsrichtung wirkt. Nach dem zweiten Newtonschen Axiom \( F = m \cdot a \) bewirkt eine Kraft \( F \) eine Beschleunigung \( a \) auf ein Objekt mit Masse \( m \). Diese Beschleunigung können wir in unserer Simulation berücksichtigen, indem wir sie in den „Spielregeln“ bei der neuen Berechnung von \( a_{x, neu} \) und \( a_{y, neu} \) addieren.
Schauen wir uns also erst einmal an, wie man die Kraft beschreiben kann, die durch die Luftreibung auf unseren Ball wirkt. Diese Kraft der Luftreibung nennen wir hier \( F_{Luft} \).
Auch diese Kraft modellieren wir. D.h. wir nutzen eine einfache Formel, die nicht alle Effekte der Natur berücksichtigen kann – aber für unsere Zwecke gut passt (wenn unser Ball mit Schallgeschwindigkeit fliegen würde, würde diese Beschreibung vermutlich nicht mehr so gut passen).
Wir nutzen diese Formel für die Luftreibungskraft: \( F_{Luft}=\frac{1}{2}\cdot A\cdot c_w\cdot \rho_{Luft}\cdot v^2 = konst_{Luft} \cdot v^2 \)
Hierbei ist:
| \( F_{Luft} \) | die Luftreibungskraft (genauer: ihr Betrag) |
| \( A \) | die Querschnittsfläche des Objekts in Flugrichtung. Je größer das Objekt ist, desto größer die die Luftreibungskraft, die auf es wirkt. Für die Querschnittsfläche einer Kugel gilt z.B.: \( A=\frac{1}{2}\cdot\pi\cdot r^2 \) mit \( r\): Radius der Kugel |
| \( c_w \) | Luftwiderstandskoeffizient (auch Luftwiderstandsbeiwert oder einfach \( c_w \)-Wert) Ist abhängig von der Form des Objektes. Unter dieser Tabelle findest du verschiedene Beispielwerte. Für einen Papiertrichter könnt ihr \( c_w = 0.75 \) verwenden. |
| \( \rho_{Luft} \) | Dichte der Luft. Für normale Bedingungen können wir nutzen: \( \rho_{Luft}= 1,225 \frac{kg}{m^3} \) |
| \( v \) | Die Geschwindigkeit des Objekts. |
Beispiele für den \( c_w \)-Wert:
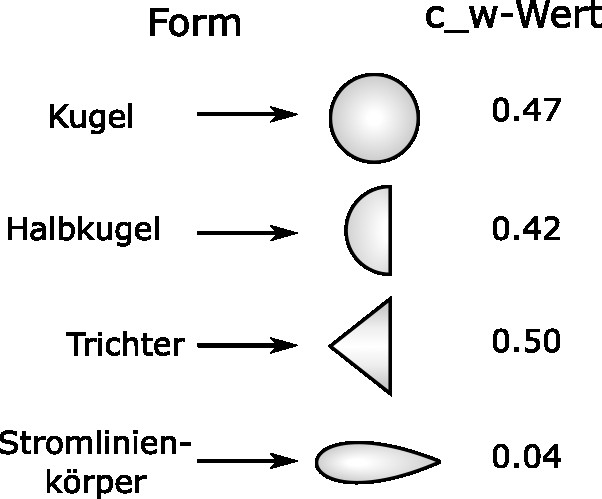
Konkrete Hinweise zur Simulation mit Luftreibung findet ihr hier.
Magnus-Effekt
Auch wenn wir Luftreibung in unserem Modell hinzufügen, bleibt unser Modell ein Modell – berücksichtigt also nicht alle Effekte, die es in der echten Welt geben kann. Ein Beispiel für einen solchen Effekt ist der Magnus-Effekt:
Objekte, die sich drehen, fliegen anders. Beispiele hierfür sind eine „Bananenflanke“ im Fußball oder ein „angeschnittener“ Ball im Tischtennis. In diesem Video findest du Beispiele und eine Erklärung hierzu:
Noch mehr Effekte
Auf dieser Seite hast du nun verschiedene Effekte kennengelernt, die es in der Natur gibt, die unser einfaches Modell des Wurfs aber nicht berücksichtigt.
Es gäbe sogar noch mehr – aber hier verraten wir zunächt nicht mehr 😉 Fallen euch weitere Effekte ein, die es in der realen Welt gibt, die aber nicht Teil des Modells sind?
